旋回半径・旋回率
意外と、旋回半径や旋回率の計算の仕方って調べても具体的な計算の仕方が分からないものです。必要としてる人ってパイロットやら管制官やら多いと思うのですが、、、
パイロット電卓
とはいえ、まぁこれからやるような手計算なんかしなくても、ttmsoftwareさんの 「パイロット電卓」 を使用すると便利。私はもうこのサイトがないと生きていけない身体になってしまいました。
それでは、どういう計算で旋回半径・旋回率を出せるのかを以下に示します。
旋回半径・旋回率の公式
何よりもまずは結論から示します。旋回半径 $r=\dfrac{V^2}{g\tan\phi}$
旋回率 $\omega=\dfrac{V}{r}$
ただし、単純に数字を入れるだけではいけません。
「速度 V」 は 「真大気速度 TAS」を使用し、通常使用する単位は[kt]
「バンク Φ」は通常使用する単位が[degree]です。
それをこの式に当てはめるには単位に注意が必要です。
旋回半径 $r[nm]=\dfrac{(TAS[kt])^2}{g[nm/h^2]\times\tan\bigl(\phi[deg]\times\dfrac{\pi}{180}\bigr)}$
旋回率 $\omega[deg/sec]=\dfrac{v}{r}=\dfrac{TAS[kt]}{3600}\times\dfrac{1}{r[nm]}\times\dfrac{180}{\pi}$
なお、 重力加速度 $g=9.80665[m/s^2]=68625.37011[nm/h^2]$
メインは以上です。
これより先は趣味の領域です。
特に見る必要もありません。
以下はこの式の導出、また、IASや高度まで含めた内容からの計算などを記します。
等速円運動の公式
使用する公式自体は基礎物理程度の簡単な計算です。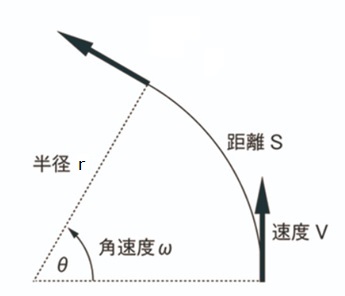
角速度 $\omega=\dfrac{\theta}{t}=\dfrac{V}{r}$
距離 $S=r\omega t$
(向心加速度)$=r\omega^2=\dfrac{V^2}{r}$
(向心力)$=m\dfrac{V^2}{r}$
航空機の旋回について
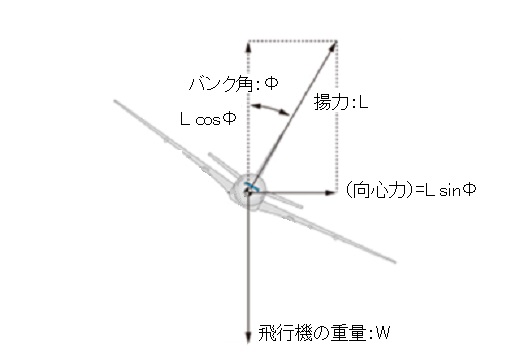
外側にも内側にも滑っていない旋回を「定常旋回」といいます。
バンク角 $\phi $ の定常旋回のとき、
1 上の図より、鉛直縦方向の力のつり合いは
$L \cos\phi = W$
2 上の図より、向心力は
$(向心力) =L \sin\phi$
3 向心力は公式より
$(向心力)=m \dfrac{V^2}{r}=\dfrac{W}{g} \dfrac{V^2}{r} $
また、揚力Lと実際の重さWとの比を「荷重倍数 n」といいます。世間一般的に言うGです。
荷重倍数 $n =\dfrac{L}{W}=\dfrac{1}{\cos{\phi}} $
2と3の、向心力の二つの式より、
$L \sin\phi=m \dfrac{V^2}{r}=\dfrac{W}{g} \dfrac{V^2}{r} $
整理すると
旋回半径 $r=\dfrac{WV^2}{gL \sin \phi}$
荷重倍数の式を代入して式を簡単にすれば
旋回半径 $r=\dfrac{V^2}{g\tan\phi}$
旋回率 $\omega=\dfrac{V}{r}=\dfrac{g\tan\phi}{V}$
ちなみに、揚力の式 $L=\dfrac{1}{2}C_L\rho SV^2 $ を代入すると、
旋回半径 $r=\dfrac{2}{g\rho C_L \sin \phi}\times\dfrac{W}{S}$ となり、
翼面荷重を小さくすれば旋回半径が小さくなることもわかる。
高度や気温、IAS等も含めて旋回半径・旋回率を求める具体的な計算方法
高度 $h=3000$ [ft]、地上気温 $T=10$ [℃]、バンク角 $\phi=30$ [deg]、IAS $V=120$ [kt] とします。高度 $h$ における外気温度 $T_{out}$ は、
圏界面(36089.24 ft)以下の高度とした場合、
$T_{out}=T-0.0019812 \times h $
圏界面(36089.24 ft)以上の高度とした場合、
$T_{out}=T-0.0019812 \times 36089.24 $
なので、外気温度 $T_{out}$ は、
$T_{out}=10-0.0019812 \times 3000 = 4.0564$ [℃]
温度比 $\theta$ は、
$\theta=\dfrac{T_{out}+273.15}{T+273.15}$
なので、温度比 $\theta$ は、
$\theta=\dfrac{4.0564+273.15}{10+273.15}=0.9790090058$
圧力比 $\delta$ は、
圏界面(36089.24 ft)以下の高度の場合、
$\delta=\theta^{ 5.25588}$
圏界面(36089.24 ft)以上の高度の場合、
$\delta=0.22336087\times e^{\dfrac{36089.24-h}{20805.825}}$
なので、圧力比 $\delta$ は、
$\delta=0.9790090058^{ 5.25588}=0.8944909103$
密度比 $\sigma$ は、
圏界面(36089.24 ft)以下の高度の場合、
$\sigma=\theta^{ 4.25588}$
圏界面(36089.24 ft)以上の高度の場合、
$\sigma=0.29708\times e^{\dfrac{36089.24-h}{20805.825}}$
なので、密度比 $\sigma$ は、
$\sigma=0.9790090058^{ 4.25588}=0.9136697466$
CAS=IASとすると、CAS=V
CAS⇒TASの公式より、
$ TAS=\sqrt{ \biggl[ \Bigl( \bigl[ (CAS^2 \dfrac{\rho_0}{P_0} \dfrac{\gamma-1}{2\gamma}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P_0}{P} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{P}{\rho} \times \dfrac{2\gamma}{\gamma-1} } $
$CAS=120[kt]=\dfrac{120\times6076.1155}{3600}[ft/s]$ 、
$P_0=2116.2166[lbs/ft^2]$ 、
$P=P_0\times\delta=2116.2166\times0.8944909103=1892.9365129259$ 、
$\rho_0=0.002376892[slugs/ft^3]$ 、
$\rho=\rho_0\times\sigma=0.002376892\times0.9136697466=0.0021716943$ 、
$\gamma=1.4$ 、
を代入すると、
$ TAS=211.7[ft/s]=125.4[kt]$
旋回半径 $r=\dfrac{V^2}{g\tan\phi}$ の公式より、
$TAS=125.4[kt]$
重力加速度 $g=68625.37011[nm/h^2]$
バンク角$\phi=30[deg]=30\times\dfrac{\pi}{180}[radian]$
を代入すると、
$r=0.396[nm]$
旋回率 $\omega=\dfrac{v}{r}$ の公式より、
$\omega=\dfrac{TAS}{3600}\times\dfrac{1}{r}\times\dfrac{180}{\pi}$
$=5.029[deg/s]$