航空機のプロペラ
プロペラの役割
プロペラシャフトの回転エネルギーを、プロペラの直径とほぼ等しい空気塊を加速することにより、推力にすること。プロペラが推力の生成に影響を与える変数
・直径・ブレードの枚数
・ブレードの角度
プロペラの生成する推力について
飛行機の翼は、「対気速度」の二乗に比例した揚力を生み出し。プロペラのブレードは、「回転速度」と「前進速度」の合成により、推力を生み出します。
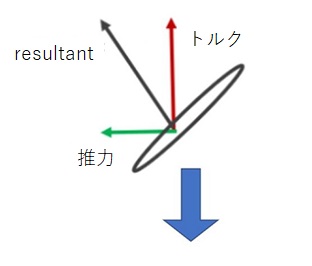
出典:AeroToolBox
プロペラの推力は、「プロペラの直径とほぼ等しい空気塊」を加速したその反力です。
よって、この運動量は加速した空気の質量と速度の積になります。
(推力)=(空気の質量)×(速度)
つまり、ブレードをできるだけ大きくすればするほど、加速できる空気量が多くなるので、効率が良い。
また、プロペラ効率 $\eta=\dfrac{(推力を生成するために利用可能な動力)}{(エンジンシャフトの出力)}$
一般的に、最も効率的で適切なプロペラ効率は0.80~0.85程度に設計されている。
なお、
(推力を生成するために利用可能な仕事量)
=(エンジンが生成する総仕事量)-(プロペラを回すのに必要な分)
(航空機を一定の速度で飛行させ続けるために必要な仕事量)
=(抗力)×(速度)
抗力は、高度一定の定常飛行時、速度の変数になるので、
(航空機を一定の速度で飛行させ続けるために必要な出力)も速度の関数です。
プロペラのピッチとは
・平面に対するプロペラブレードの角度。・プロペラが1回転中に前進する距離。
・プロペラが空気から取り出す「bite」。
・車でいうギア fine pitch (low gear) - coarse pitch (high gear).
fine pitch:低ピッチ・簡単に回転する・高速rpm・短い距離を移動
coarse pitch:高ピッチ・エンジンが動作する速度を制限・低rpm・一掻きが大きい
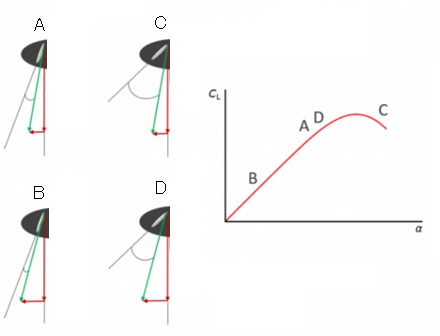
出典:AeroToolBox
A:低速・低ピッチ
低対気速度で効率的に推力を生む。
B:高速・低ピッチ
Aよりも迎え角が低く、ブレードの揚力が減少、それに応じて推力も減少。
C:低速・高ピッチ
ブレードの迎角が失速角に入ると揚力を生まず、推力が低い。
D:高速・高ピッチ
大きな対気速度成分の結果として、迎え角が失速から離れたポイントに減少している。ブレードは効率的に推力を生む。
例 )
・離陸・着陸
低速な飛行。最大の推力を生み出すには、低ピッチが良い。
・巡航
比較的高速な飛行。高ピッチが効率的。
・上昇
離陸時より高ピッチ、巡航より低ピッチが効率的。
プロペラ先端の速度
プロペラ先端の回転速度: $V_{rot}=\pi \times (直径 d) \times rps$プロペラ先端の並進速度: $V_{trans}=AirSpeed$
プロペラ先端の螺旋速度: $V_{tip-helical}=\sqrt{{V_{rot}}^2+{V_{trans}}^2}$
プロペラトルク
直線運動における $(力 F)=(質量 m)\times(加速度 \alpha)$ は、回転運動において $(トルク T)=(慣性モーメント I)\times(角加速度 α)$
慣性モーメントは回転中心に対する質量の分布。
フィギュアスケートの選手が手を伸ばしていると回転が遅く、手を縮めると速くなるのと同じ。
$(慣性モーメント I)=\dfrac{角運動量 L}{角速度 \omega}=(質量 m)\times(回転軸からの重心距離 r)^2$
プロペラの直径が大きいほど、ハブから重心が離れ、慣性モーメントは距離の2乗で増加する。
$(必要なトルク T)=(慣性モーメント I)\times (角加速度 α) = m \times r^2 \times (回転加速度 \alpha)$
プロペラの前進比は、流体速度(対気速度)とプロペラ先端速度の比
プロペラは「航空機の前進速度」や「プロペラの回転速度」に関係なく、前進比が同じだと迎角も同じになる。
$(前進比 J)=\dfrac{(対気速度 V)}{(プロペラの回転速度 n) \times (プロペラ直径 d)}$
プロペラチャート
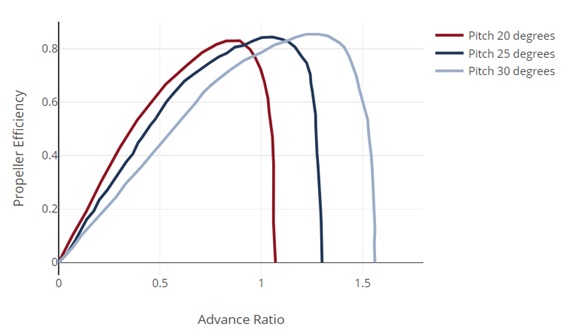
出典:AeroToolBox
横軸:前進比 、 縦軸:プロペラ効率(プロペラ直径)、(ブレードのピッチ)、(ブレードの枚数)の違いによるグラフの変動を見るもの
推力計算の例
4300rpm 、直径1.7m 、TAS120kt 、ブレードピッチ25度、プロペラシャフトの減速ギア比 2.27
プロペラ効率のグラフは上のグラフ、とした時の推力について
$V=120[kt]=61.73[m/s]$
$4300[rpm]=4300/60=71.67[rps]$
プロペラの回転速度 $V_{prop}=71.67/2.27=31.6[rps]$
前進比 $J=\dfrac{V}{n\times d}=\dfrac{61.73}{31.6\times 1.7}=1.15$
前進比 1.15のとき、グラフより、プロペラ効率 $\eta=0.816$
推力 $F=\dfrac{(エンジンの仕事量) \times (プロペラ効率)}{(速度)} $
$= \dfrac{45.2 \times 1000 \times 0.816}{61.7} = 598[N]$