航空機の座標軸
地心三次元直交軸
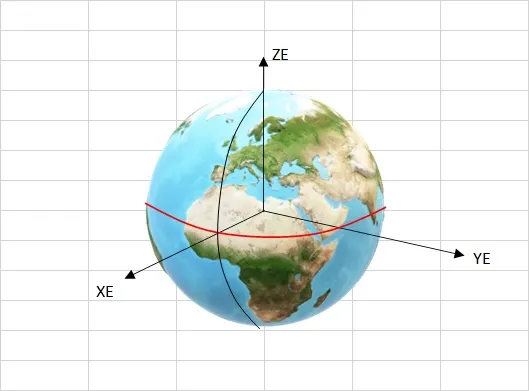
出典:国土地理院ウェブサイト https://www.gsi.go.jp/sokuchikijun/datum-main.html
原点が地球の重心
X軸が本初子午線と赤道との交点の方向
Y軸が東経90度の方向
Z軸が北極(地軸の北端)の方向
GPSの位置座標として使用
※日本が採用している世界測地系(ITRF:国際地球基準座標系)ではIERS基準子午線(IERS Reference Meridian)を本初子午線としており、IERS基準子午線はグリニッジ子午線(英国のグリニッジ天文台のエアリー子午環を通る子午線)の102mほど東を通過している。
地面固定軸
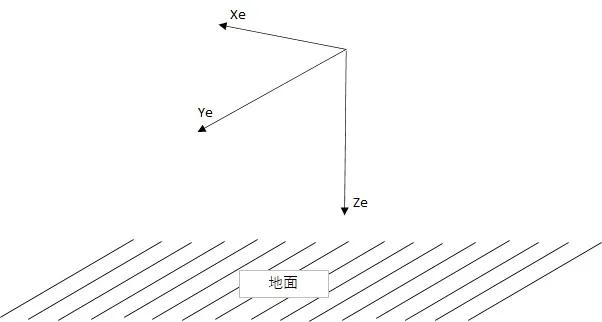
$x_e - y_e$ 面が水平面(地面と平行)
$z_e$ 軸が鉛直方向
地面を基準とした位置を示す。
機体固定軸
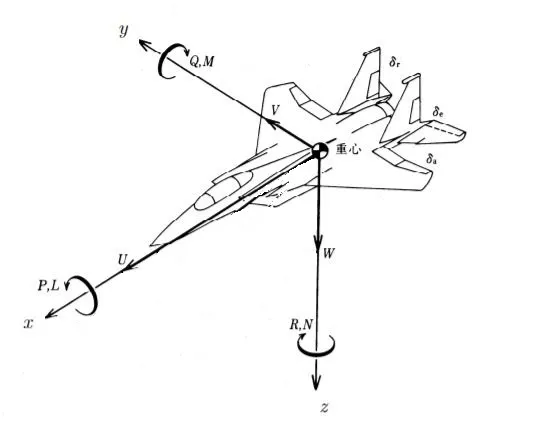
原点が機体の重心
X軸が機種方向
Y軸が右翼方向
Z軸が機体下面方向
地面固定軸を基準として、
$x_e$ 軸を固定した回転、ロール角 $\phi$
$y_e$ 軸を固定した回転、ピッチ角 $\theta$
$z_e$ 軸を固定した回転、ヨー角 $\psi$ を加えた変化形が機体固定軸となる。
安定軸
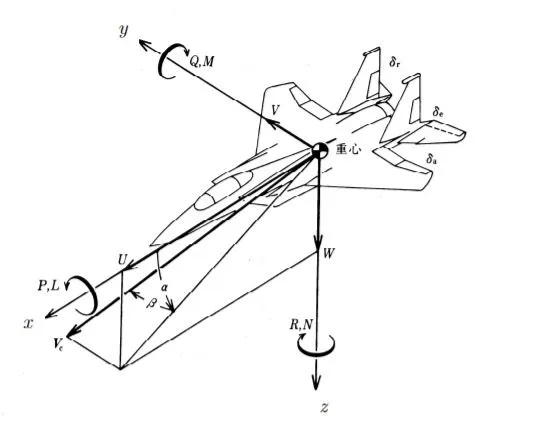
原点が機体の重心
X軸が巡航時の速度の方向
Y軸がX軸と直角に右翼の方向
Z軸がx-y面と直角に機体下面の方向
機体固定軸を基準として、
迎角 $\alpha$ 及び、横滑り角 $\beta$ を加えた変化形が安定軸
地面固定座標系と機体固定座標系の関係
一般的に、直交座標系 を 極座標系 で示す場合$ \begin{cases} x=r \sin \theta \cos \phi \\ \\ y=r \sin \theta \sin \phi \\ \\ z=r \cos \theta \\ \\ r= \sqrt{x^2+y^2+z^2} \end{cases} $
位置ベクトル $(x,y,z)$
↓微分 ↑積分
速度ベクトル $(x',y',z')=(u,v,w)$
↓微分 ↑積分
加速度ベクトル $(x",y",z")=(\dot{u},\dot{v},\dot{w})$
各軸における回転ベクトル $(\phi,\theta,\psi)$
↓微分 ↑積分
角速度ベクトル $(\phi',\theta',\psi')=(p,q,r)$
↓微分 ↑積分
角加速度ベクトル $(\phi",\theta",\psi")=(\dot{p},\dot{q},\dot{r})$
機体固定座標系 と 地面固定座標 の関係①
$\cos$ を $c$、$\sin$ を $s$ と示します。
$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} c\theta \ c\psi & c\theta \ s\psi & -s\theta \\ s\phi \ s\theta \ c\psi \ -c\phi \ s\psi & s\phi \ s\theta \ s\psi +c\phi \ c\psi & s\phi \ c\theta \\ c\phi \ s\theta \ c\psi +s\phi \ s\psi & c\phi \ s\theta \ s\psi \ -s\phi \ c\psi & c\phi \ c\theta \end{pmatrix} \begin{pmatrix} x_e \\ y_e \\ z_e \end{pmatrix} $
機体固定座標系 と 地面固定座標 の関係②
$ \begin{pmatrix} x_e \\ y_e \\ z_e \end{pmatrix} = \begin{pmatrix} c\theta \ c\psi & s\phi \ s\theta \ c\psi \ -c\phi \ s\psi & c\phi \ s\theta \ c\psi +s\phi \ s\psi \\ c\theta \ s\psi & s\phi \ s\theta \ s\psi +c\phi \ c\psi & c\phi \ s\theta \ s\psi \ -s\phi \ c\psi \\ -s\theta & s\phi \ c\theta & c\phi \ c\theta \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} $
$ \Longleftrightarrow \begin{pmatrix} x_e' \\ y_e' \\ z_e' \end{pmatrix} = \begin{pmatrix} c\theta \ c\psi & s\phi \ s\theta \ c\psi \ -c\phi \ s\psi & c\phi \ s\theta \ c\psi +s\phi \ s\psi \\ c\theta \ s\psi & s\phi \ s\theta \ s\psi +c\phi \ c\psi & c\phi \ s\theta \ s\psi -s\phi \ c\psi \\ -s\theta & s\phi \ c\theta & c\phi \ c\theta \end{pmatrix} \begin{pmatrix} u \\ v \\ w \end{pmatrix} $
$ \Longleftrightarrow \begin{pmatrix} x_e' \\ y_e' \\ h_e' \end{pmatrix} = \begin{pmatrix} c\theta \ c\psi & s\phi \ s\theta \ c\psi \ -c\phi \ s\psi & c\phi \ s\theta \ c\psi +s\phi \ s\psi \\ c\theta \ s\psi & s\phi \ s\theta \ s\psi +c\phi \ c\psi & c\phi \ s\theta \ s\psi -s\phi \ c\psi \\ s\theta & -s\phi \ c\theta & -c\phi \ c\theta \end{pmatrix} \begin{pmatrix} u \\ v \\ w \end{pmatrix} $
ここで、$h_e'$は高度の昇降率を示す
ちなみに、
オイラー角と機体角速度の関係①
$ \begin{pmatrix} p \\ q \\ r \end{pmatrix} = \begin{pmatrix} 1 & 0 & -\sin \theta \\ 0 & \cos \phi & \sin \phi \cos \theta \\ 0 & -\sin \phi & \cos \phi \cos \theta \end{pmatrix} \begin{pmatrix} \phi' \\ \theta' \\ \psi' \end{pmatrix} $
オイラー角と機体角速度の関係②
$ \begin{pmatrix} \phi' \\ \theta' \\ \psi' \end{pmatrix} = \begin{pmatrix} 1 & \dfrac{\sin \phi \sin \theta}{\cos \theta} & \dfrac{\cos \phi \sin \theta}{\cos \theta} \\ \\ 0 & \cos \phi & -\sin \phi \\ \\ 0 & \dfrac{\sin \phi}{\cos \theta} & \dfrac{\cos \phi}{\cos \theta} \end{pmatrix} \begin{pmatrix} p \\ q \\ r \end{pmatrix} $