航空機の速度
IAS : 指示対気速度 indicated
計器に表示されている速度ピトー管で測定した動圧を表示している。
ピトー管は飛行機の姿勢などの影響をできるだけ受けない場所に取り付けられているが、どうしても「取り付け誤差(位置誤差)」や「機体姿勢の変化による誤差(計器誤差)」ができてしまう。
これを修正したものが、
CAS : 較正対気速度 calibrated
IASから、位置誤差・計器誤差の補正を加えた速度。主にT/OやL/D時の飛行規定等に用いられる。
しかし、現代では大体の飛行機は情報をコンピュータ処理しているので、軽飛行機やグライダーでもない限り、IAS=CASと考えてよい。
軽飛行機などでは基本的に各機種ごとPOHにIAS⇔CASの換算表が添付されている。
TAS : 真対気速度 true
言葉の通り。空気が飛行機を横切る真の速度。
パイロットは旋回半径や風の影響などを考えるときに結構使う。
乱れていない大気と航空機との相対速度
一般的にCAS(較正対気速度)に空気密度比の修正をして得られる。
EAS : 等価対気速度 equivalent
航空機構造の強度計算などに使う用の速度。CASに空気の圧縮性の誤差を補正した速度。
高度も低く、速度も小さい場合,圧縮性を無視でき,CAS=EASとなる。
海面上標準大気状態ではCAS=EAS=TASとなる。
GS:対地速度 ground
地表面に対する相対的な水平速度TASに風の影響を加味して求められる。
Mach:マッハ数
音速と飛行機の速度の比亜音速:マッハ数 0.75以下
遷音速:マッハ数 0.75~1.25ぐらい
超音速:マッハ数 1.2~5.0
極超音速:マッハ数大体5以上
飛行機の速度について の計算
$C_{pitot}$ : ピトー管係数 通常1になるように設計されており、考える必要がないように配慮されている。圧力:$P_0 = 101325 [Pa] =101325 [kg/m・s^2] =14.6959[lb/in^2]=2116.2166 [lb/ft^2]$
密度:$\rho_0 = 1.225 [kg/m^3] =0.00237689 [slug/ft^2]$
比熱比:$\gamma = 1.4$
速度:$1[kt] = 0.514444 [m/s] =1.6878 [ft/s]$
$ TAS=\sqrt{\dfrac{2 \gamma P_0}{( \gamma -1) \rho_0 } ( ( \dfrac{P_t - P_s}{P_0} +1)^{ \dfrac{ \gamma -1}{ \gamma } }-1 )}=C_{pitot}\sqrt{\dfrac{2(P_t-P_s)}{\rho}}$
TAS ⇒ CAS , Mach , EAS
$ EAS=TAS\times\sqrt{\sigma}$$ CAS=\sqrt{ \biggl[ \Bigl( \bigl[ (TAS^2 \dfrac{\rho}{P} \dfrac{\gamma-1}{2\gamma}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P}{P_0} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{P_0}{\rho_0} \times \dfrac{2\gamma}{\gamma-1} } $
$ Mach=\dfrac{TAS}{s}=TAS\sqrt{\dfrac{\rho}{\gamma P}}=\dfrac{TAS}{a_0 \sqrt{\theta}}=\sqrt{\dfrac{T_0-T}{\gamma-1}\dfrac{2}{T}}=\sqrt{\dfrac{2}{\gamma-1}\bigl( \dfrac{1}{\theta}-1 \bigr)}$
CAS ⇒ TAS , Mach , EAS
$ TAS=\sqrt{ \biggl[ \Bigl( \bigl[ (CAS^2 \dfrac{\rho_0}{P_0} \dfrac{\gamma-1}{2\gamma}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P_0}{P} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{P}{\rho} \times \dfrac{2\gamma}{\gamma-1} } $$ Mach=\sqrt{ \biggl[ \Bigl( \bigl[ (CAS^2 \dfrac{\rho_0}{P_0} \dfrac{\gamma-1}{2\gamma}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P_0}{P} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{2}{\gamma-1} } $
$ EAS=\sqrt{ \biggl[ \Bigl( \bigl[ (CAS^2 \dfrac{\rho_0}{P_0} \dfrac{\gamma-1}{2\gamma}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P_0}{P} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{P}{\rho_0} \times \dfrac{2\gamma}{\gamma-1} } $
Mach ⇒ CAS , TAS , EAS
$ CAS=\sqrt{ \biggl[ \Bigl( \bigl[ (Mach^2 \dfrac{\gamma-1}{2}+1)^{\frac{\gamma}{\gamma-1}} -1 \bigr] \times \dfrac{P}{P_0} +1 \Bigr)^{\frac{\gamma-1}{\gamma}} -1 \biggr] \times \dfrac{P_0}{\rho_0} \times \dfrac{2\gamma}{\gamma-1} } $$ TAS=a_0 \times Mach \times \sqrt{\theta}$
$ EAS=a_0 \times Mach \times \sqrt{\delta}=TAS \times \sqrt{\sigma}$
TAS ⇒ GS
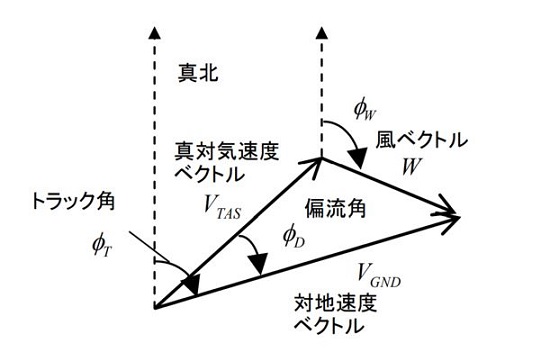
$ GS=TAS \times \cos \phi_D +W \cos (\phi_W-\phi_T)$
$ \phi_D=\sin^{-1} \Bigl[ \dfrac{W}{TAS}\sin (\phi_W-\phi_T) \Bigr] $
パイロットが行っている上昇の仕方
パイロットは、「低高度ではIAS一定で上昇」
「高々度(3万ft近く以上)ではマッハ数一定で上昇」します。
なぜでしょう?
わざわざ計器を2つに増やしてややこしくしているには当然理由があります。
つまり、「IAS」だけで上昇していると不具合が出てくるのです。
それを解決するのに丁度良かったから、わざわざ「Mach計」なんてものを追加して使うのです。
「IAS」は「動圧」を表示しているものです。
つまり「IAS一定」とは、「動圧が一定」ということです。
空気は高度が高くなるにつれて、薄くなります。
そのため「IAS一定で上昇」とは、
「高度が上がって空気がどんどん薄くなっていってるのに同じ動圧を得ている」ということです。
薄い空気で同じ圧力を得るためには、その分もっと多くの空気が必要です。
つまり「TAS」で考えてみると、「TAS的には加速しながら上昇」していることになります。
高校物理での「位置エネルギー」と「速度エネルギー」の関係を覚えていますか?
同じエネルギーの総量なら、高い時が遅く、低い時が速いはずです。
それなのに、「高いところへ加速しながら行こう」とするなんて、どんだけ大きなエネルギーが必要になるかたまったもんではありません。
一方で、マッハ数とは「音の速さに対する割合」です。
そして音の速さは( $a=a_0\times\sqrt{\theta}$ ) の式からわかるように、「温度に依存する」値です。
対流圏内( $h_p$ < 36089.24ft(11000m))では高度が上がると温度が低下します。
つまり、「高度が上がると音の速さは遅く」なります。
ここで、マッハ数とTASの関係を思い出してください。
$Mach=\dfrac{TAS}{a}$ の式です。
マッハ数一定で、音の速さが遅くなるなら、TASの値も小さくなります。
つまり「TAS」で考えてみると、「TAS的には減速しながら上昇」していることになります。
減速しながら上昇する。
つまり、「速度エネルギー」が「位置エネルギー」に変換されるのでとても効率的です。上昇率がとても大きく変わります。
そして、成層圏内下層 ( 36089.24ft(11000m)< $h_p$ <65616.8ft (200000m) )では温度は一定なので、Mach一定で上昇することはTAS一定で上昇することになります。
n-V線図

横軸:速度(EAS)
$V_A$ : 設計運動速度:制限荷重を超えることもなく、失速に対しても最大限の余裕をとれる速度。
$V_S$ : 失速速度
$V_{S1}$ : フラップ展開時の失速速度
$V_{FE}$ : フラップ展開時の制限速度
$V_C$ : 設計巡航速度:機体の負の制限荷重が最大に取れなくなる速度。
$V_{NO}$ : 最大巡航速度
$V_{NE}$ : 超過禁止速度
$V_D$ : 設計急降下速度