航空機に係る力
揚力:L 、 抗力:D 、 自重:W 、 推力:T揚力 L
揚力とは 「機首方向に垂直に作用する力」 のことを言います。物体の回りを空気が流れると、圧力の変動が生じます。
揚力は、この圧力変動の結果生まれる力です。
揚力の大部分は飛行機の翼によって生成されます。
揚力 $L=\dfrac{1}{2}C_L \rho S V^2$
変形すると、
揚力係数 $C_L=\dfrac{2L}{\rho S V^2}=\dfrac{L}{pS}$
また、空気の粘性を考慮するならば(レイノルズ数を用いるならば)、無次元係数$K$、実数$d$とすると
揚力 $L=K \rho S V^2 {(R_e)}^d$
とも書くことができる。
定常飛行時、$L=W$なので
標準大気・高度一定において、揚力係数は速度の二乗に反比例する。

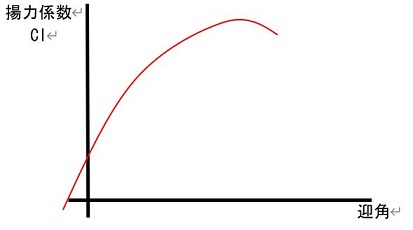
また、迎え角「$\alpha$」とは、「翼弦の空気流に対する角度」のことであり、
誘導迎角とは「見かけの迎え角」または「後縁付近の平均線を延長した線の角度」のことを言い、
誘導迎角 ${\alpha}_i=\dfrac{吹きおろし速度\omega}{V}=\dfrac{C_L}{\pi A}$ の式が成り立つ
抗力 D
抗力とは 「飛行方向と反対に作用する力」 のことを言います。飛行機は空気を媒体にして力を生じているため、「空気抵抗」とも言えます。
航空力学は、この「抗力」をどう解消するかの学問です。
つまりこいつが「敵」です。
抗力は考えれば考えるだけ出てくるので、超複雑、かつめんどい。そんで極めて行ったら終わりがありません。
とりあえず一番簡単な表現は
$D=\dfrac{1}{2}C_D \rho S V^2=qSC_D$
⇒ $C_D=\dfrac{2D}{\rho S V^2}=\dfrac{D}{pS}$
細かく表現すると、
(抗力)= (有害抗力 $C_{Dp}$ ) + (誘導抗力 $C_{Di}$ )
={(摩擦抗力)+(圧力抗力)+(干渉抗力)}+ (誘導抗力)
= (ゼロリフト抗力) +(リフト誘導抗力)
=[{ (胴体)+ (主翼)+ (垂直尾翼) + (水平尾翼) + (その他いっぱい) }]+(誘導抗力)
・有害抗力 $C_{Dp}$ :「物体」が「空気」と相互作用した結果として生まれる抗力。
揚力の発生とは関係なく存在する抗力なので、ゼロリフト抗力ともいう。
・誘導抗力 $C_{Di}$ :揚力が発生する副産物。揚力が発生すると必ず生まれる。必要悪。
(造波抗力:衝撃波による抗力。一般にマッハ0.8を超えると、翼表面では部分的に音速を超えて衝撃波が発生する。低速域では無視していい。船が水面に波を立てて進む状態と似ているので,造波抗力または造波抵抗という。)
● 有害抗力(ゼロリフト抗力)の概念
・摩擦抗力
空気の粘性により発生する、空気と機体の間の摩擦力。
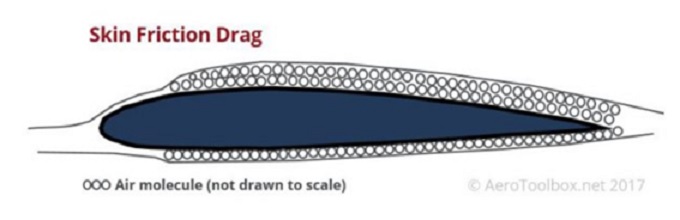
出典:AeroToolBox
平板の摩擦係数 $C_f$
i ) 層流 $(R_e<5.3 \times 10^5 )$ のとき
$C_f=\dfrac{1.328}{\sqrt{R_e}}$
ii) 遷移流 $(5.3 \times 10^5<R_e<2 \times 10^8 )$ のとき
$C_f=\dfrac{0.455}{(log_{10}R_e)^{2.58}} -\dfrac{1700}{R_e}$
iii) 乱流 $(2 \times 10^8<R_e )$ のとき
$C_f=\dfrac{0.455}{(log_{10}R_e)^2.58}$
また、サザーラントの公式より
$\mu=\mu_0 \times \Bigl( \Bigl( \dfrac{T}{T_0} \Bigr)^{1.5} \times \dfrac{T_0+S}{T+S}\Bigr)$
なお、標準大気のとき
$\mu_0=1.7894\times10^{-5} [Pas]$、 $T_0=288.15 [K]$、
サザーラント定数 $S=110.4$
動粘性係数 $\nu=\dfrac{粘性係数 \mu}{密度 \rho}$
レイノルズ数 $R_e=\dfrac{慣性力}{粘性力}=\dfrac{\rho\times TAS\times (代表長さ l)}{\mu} =\dfrac{TAS\times l}{\nu}$
臨界レイノルズ数 $R_e=5.3\times10^5$
・圧力抗力
物体の形状による圧力分布の影響。
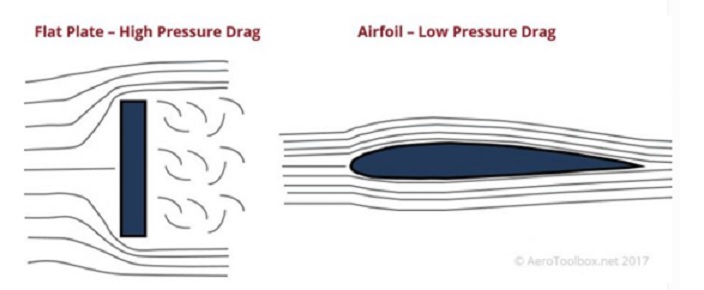
出典:AeroToolBox
・干渉抗力
互いに接触している物体どうしの相互作用から発生する抵抗力。
例えば、「翼の抗力」と「胴体の抗力」をそれぞれ個別に出して足した数字よりも、「翼と胴体を組み合わせた機体としての抗力」の方が大きくなります。その差が干渉による抗力。
● 各部位の有害抗力(ゼロリフト抗力)
・胴体のゼロリフト抵抗係数
$C_{D_{0(fus)}}=R_{wf} \times C_{f(fus)} \times \left(1+60 \times (\dfrac{d_f}{l_f})^3+0.0025\times(\dfrac{l_f}{d_f}) \right) \times \dfrac{S_{wetF}}{Sref}$
・主翼のゼロリフト抵抗係数
$C_{D_{0(wing)}}=R_{wf} \times R_{LS} \times C_{f(wing)} \times \left(1+L^* \times \dfrac{t}{c}+100 \times (\dfrac{t}{c})^4 \right) \times \dfrac{S_{wetW}}{Sref}$
・水平尾翼のゼロリフト抵抗係数
$C_{D_{0(H-tail)}}=R_{wf} \times R_{LS} \times C_{f(H-tail)} \times \left(1+L^* \times \dfrac{t}{c}+100 \times (\dfrac{t}{c})^4 \right) \times \dfrac{S_{wetH-tail}}{Sref}$
・水直尾翼のゼロリフト抵抗係数
$C_{D_{0(V-tail)}}=R_{wf} \times R_{LS} \times C_{f(V-tail)} \times \left(1+L^* \times \dfrac{t}{c}+100 \times (\dfrac{t}{c})^4 \right) \times \dfrac{S_{wetV-tail}}{Sref}$
・その他いろいろの形状協力 & 干渉抗力 補正係数 $K_c$
$R_{wf}$:翼/胴体 干渉係数 1.0で問題ない。
$C_{f(fus)}$:乱流平板摩擦係数
$d_f$:胴体の直径 胴体が楕円なら相当直径の$\sqrt{\dfrac{4}{\pi}\times S_{fus_{MAX}}}$
$l_f$:胴体の長さ
$S_{fus_{MAX}}$:胴体の最大の断面積
$S_{wet}$:空気に触れる表面積
$S_{ref}$:翼面積
$R_{LS}$:揚力面補正係数 後退角とMachによる変数 Aero toolboxのサイト で調べるとよい
$L^*$:翼厚の場所を示すパラメータ
翼厚が最大になる位置が、前縁1/3より前方のとき ⇒ $L^*=2.0$
翼厚が最大になる位置が、前縁1/3より後方のとき ⇒ $L^*=1.2$
$t$:翼厚
$c$:翼弦長
●よって、まとめると 有害抗力係数 $C_{Dp}=K_c \times {C_{D0(fus)}+C_{D0(wing)}+C_{D0(H-tail)}+C_{D0(V-tail)}}$
● 誘導抗力
誘導抗力は、揚力が発生する副産物。
主に揚力の発生に関与しているのは翼なので、これが主な原因と言える。
誘導抗力係数 $ C_{Di}=\dfrac{{C_L}^2}{\pi \times AR \times e} = L \times {\alpha}_i $
よって、TOTALの抗力係数 $C_D$ は
\begin{align} C_D &=C_{Dp}+C_{Di} \nonumber \\ &=\Bigl( K_c \times {C_{D0(fus)}+C_{D0(wing)}+C_{D0(H-tail)}+C_{D0(V-tail)}}+C_{Di} \Bigr) +\dfrac{{C_L}^2}{\pi \times AR \times e} \nonumber \\ \end{align}

このグラフのことを「drug bucket」という。
自重 W
地球上のすべての物質には質量があり、ここでいう「自重 W」は「航空機の質量に作用する地球の引力」 です。
「航空機の質量」は、「機体構造」「エンジン」「ペイロード(人、貨物、荷物)」「燃料」「搭載システム」「航空機に搭載されているその他全て」等の質量の和になります。
この中で、「燃料」は刻一刻と消費されていくため、航空機の運航中、自重は常に減少方向に変化し続けています。空中給油なんてしようものなら、自重は増加方向に変化もします。しかし、そんなことを考えていると非常に計算が煩雑になり、現代ではまだ自重の変化まで考慮できないので、「自重W=(一定)」と考えることが一般的です。
$W=nmg=(一定)$
推力 T
推力とは 「飛行方向に作用する力」 です。推力はエンジンによって生成され、抗力に打ち勝つために使用します。
パイロットは、スロットル等をコントロールすることにより、「推力と抗力の瞬間的な違い」を生み、航空機を「加速」または「減速」させます。
エンジンが空気を後方に押し込む、その反発力が、推力です。
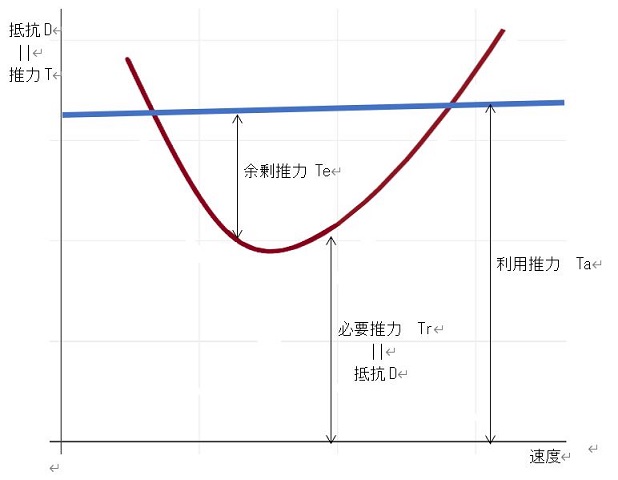
1 利用推力 available
エンジンの性能による。
どの飛行状態でも利用できる。
2 必要推力 required
抗力に打ち勝つために最低限必要な推力。
つまり抗力と同じ値のこと。
3 余剰推力 excessive
(余剰推力)=(利用推力)-(必要推力)
この力を利用して加速する。
(定格推力:エンジン強度上の制限をもとに保証される最大推力のこと。)
推力を式で表すとすれば
(推力)=(単位時間に吸い込む空気の質量)×(噴出速度−飛行速度)
また、エンジンの推進効率 $ \eta =\dfrac{2V_i}{V_i+V_j}$
$V_i$ : インテーク吸い込み速度
$V_j$ : 排気速度
4つの力のつり合いについて
i ) 定常飛行(等速直線運動)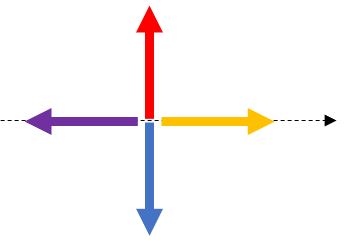
ii ) 上昇
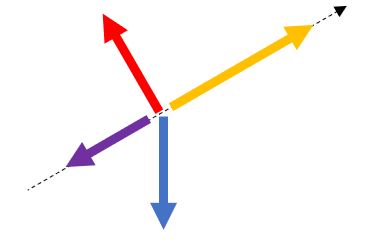
iii ) 降下
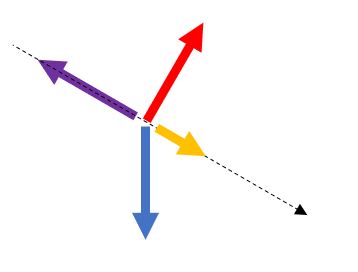
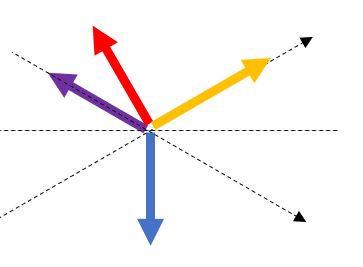
iv ) 着陸・スローフライト
定常飛行時は力が全部釣り合っている。
$L=W$ 、 $T=D$
航空機の上昇と降下時、航空機に作用する力(推力と抗力)の仕事率が、機体の位置エネルギーと運動エネルギーの増加率と等しいので、
$(T-D) \times TAS = mg \dfrac{d h_p}{d t}+m TAS \dfrac{dTAS}{dt}$